
Pete Rose batted for Newcombe and legged out an infield single after two quick outs, Brett doubled into the left-center gap to score Rose, and Kluszewski lined a single up the middle to bring Brett around. In the bottom of the inning, Lou Boudreau reached on a Brett error and scored on Mize’s triple before another Newcombe wild pitch again allowed Mize to score, giving the Fungoes the lead.īut Brecheen’s luck finally ran out in the eighth. But Mays was thrown out trying for third and Brecheen sandwiched two outs around a walk to finish the inning. George Brett opened the seventh with a triple, Ted Kluszewski singled him home, and Willie Mays doubled Brett home. The lead proceeded to ping-pong over the next three half-innings. Ernie Lombardi and Brecheen grounded into fielder’s choices at home, and Frenchy Bordagaray’s liner to center landed in the glove of Willie Mays. Newcombe would not be so lucky, as Johnny Mize opened the bottom of the sixth with a single, moved to third on Bobby Estalella’s double, and (after an intentional walk to Stan Hack) scored on a wild pitch.īut the damage could have been far worse, as though Newcombe walked Rocky Bridges to fill the bags with no outs, the Fungoes did not score again in the inning. In the top of the inning, Brecheen allowed his second hit (a Newcombe single) and second walk (to Jackie Robinson) of the game, but kept the Cashmen from scoring. The sixth saw both starters begin to crack.
#HARMONIC SERIES SERIES#
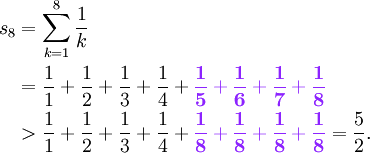
(Music, other) acoustics the series of tones with frequencies. Newcombe had allowed runners to reach base in four of the five innings, but the Fungoes left a man on three times and the bases loaded once. (Mathematics) maths a series whose terms are in harmonic progression, as in 1 + + + 2. Through five innings, with both teams scoreless, Brecheen had outpitched Newcombe, facing the minimum while allowing just a hit and a walk. Harry Brecheen, pitching Triple Crown winner, threw eight innings but wound up the loser. Briefly, the harmonic series, also referred to as the overtone series, occurs whenever you play a pitch in. As we will see, it is the basis for an effective chord voicing, to understand chord tones and tensions, scale construction and also rhythm. What started out as a pitching duel turned into a back-and-forth bat battle as both pitchers reached their limit on the mound.Īlthough Don Newcombe left the game after seven innings trailing 3-2, he wound up the winner as the Cashmen scored two runs in the top of the eighth, their bullpen holding back the Fungoes’ offense to complete a 4-3 victory. The harmonic series is probably the most fundamental aspect upon which music can be understood. In any case, it is the result that students will be tested on, not its derivation.(New year of OOTP, new fonts on the scoreboard.) Hence, using the definition of convergence of an infinite series, the harmonic series is divergent.Īlternate proofs of this result can be found in most introductory calculus textbooks, which the reader may find helpful. If we work ahead to, we obtainĪs tends to infinity, the partial sums go to infinity. Moving ahead to we find (using highlighting to bring attention to what changes are made to create our inequality) Let's look at a few of the partial sums, and see if we can find a pattern. There are a few different ways to to determine whether the harmonic series converges, but we will investigate this question using the definition of convergence above. Does it look like the partials sums are converging? That is, it plotsįor a value of n that you provide. The widget below plots the partial sums of the harmonic series for a chosen n. Plotting the Partial Sums of the Harmonic Series Absolute Convergence Implies ConvergenceĪnother useful example of a series whose convergence we can determine based on the behaviour of the partial sums is the harmonic series, whose infinite sum is given byĭo you think this infinite series converges? The terms of the sequence are monotonically decreasing, so one might guess that the partial sums would in fact converge to some finite value and hence the sequence would converge.The Contrapositive and the Divergence Test.A Motivating Problem for the Alternating Series Test.


 0 kommentar(er)
0 kommentar(er)
